Kilátáselmélet: Miért Aszimmetrikus A Piac?

Daniel Kahneman Gyors és lassú gondolkodás című művét olvasva még több értelmet nyert a piaci érzelmek aszimmetriája, azaz a volatility skew.
Mielőtt belevágnék a cikk tartalmi fejtegetésébe, egy rövid elméleti hátteret kívánok adni a Kahneman és Tversky által megalkotott kilátáselméletről.
A cikk terjedelmi korlátok miatt nem képes felölelni a teljes elméletet, így csak az általam fontosnak tartott részeket emelem ki, majd rámutatok ennek a kereskedésre gyakorolt hatására.
Kilátáselmélet vs. hasznosságelmélet
Kahneman előtt a Bernoulli féle hasznosságelmélet volt az uralkodó eszme a nyereség és veszteség értékelése során. Kahneman-ék észrevettek benne egy jelentős hibát.
"A hasznossági elmélet szerint a nyereség hasznosságát úgy kaphatjuk meg, hogy összehasonlítjuk a vagyon két állapotának hasznosságával. Például egy további 500 dollár hasznossága, amelyet az 1 millió dollár vagyonunkhoz kapunk az 1 millió 500 és az 1 millió dollár összeg hasznosságának a különbsége lesz. Ha pedig a nagyobb összeg van a birtokunkban, akkor az 500 dollár elvesztésével járó hasznosságcsökkenés ismét a két vagyoni állapot hasznosságának különbsége lesz. Ebben az elméletben a nyereségek és a veszteségek hasznossága csak az előjelben különbözhet egymástól. Ez az elmélet nem tudja megmagyarázni, hogy az 500 dollár elvesztése miért járhat nagyobb hasznosságcsökkenéssel, mint amennyivel ugyanekkora nyereség a pénzünk hasznosságát növeli - márpedig ez a helyzet."
Magyarán sokkal jobban fáj 500 dollár elvesztése, mint annak megnyerése pozitív oldalról függetlenül attól, hogy mekkora a vagyonunk. Az érzés és a megközelítés aszimmetrikus.

Nálad hogy működik?
Nézzünk rá egy példát. Melyiket választanád?
- Biztosan kapsz 9.000 dollárt vagy 90%-os valószínűséggel kapsz 10.000 dollárt?
- Biztosan elveszítesz 9.000 dollárt vagy 90%-os valószínűséggel elveszítesz 10.000 dollárt?
Az első kérdésre valószínűleg kockázatkerülő választ adtál, azaz megtartod a 9.000-et biztosan. Ugyanis a 9.000 dollár szubjektív értéke bizonyosan több, mint a 10.000 dolláros nyereség szubjektív értékének 90%-a.
A második esetben, ha a többséghez hasonlóan gondolkodsz akkor a második lehetőséget választod, azaz kockázatot vállalsz. A kockázatvállaló magatartás magyarázata az 1. kérdés kockázatkerülésére adott magyarázat tükörképe: 9.000 dollár elvesztésének negatív értéke sokkal magasabb, mint a 10.000 dolláros veszteség negatív értékének 90%-a.
Magyarán a biztos veszteséggel szemben erős ellenérzéseink vannak, ez késztet minket arra, hogy kockázatot vállaljunk.
Többek között emiatt hagyják többen futni a veszteséget, mert hátha fordul és hátha megússzák. A biztos veszteség realizálása sokkal fájdalmasabb, mint a bizonytalan veszteség x%-a. Sokkal inkább vállalsz kockázatot, ha két rossz lehetőség közül kell választanod. Érdemes ezt fejben tartani és tudatosnak lenni rá. Ez azért is fontos, mert ha nonstop ezen "ösztönök" szerint hozol kereskedési döntést, akkor matematikailag garantált, hogy le fogod a számlát darálni.

Hol tévedett Bernoulli?
Az elmélete szerint ha csak a vagyon hasznossága számít, semmi más akkor egyazon probléma kétféle, ám nyilvánvalóan egyenértékű megfogalmazására azonos döntésekkel kellene válaszolnunk. De nem ez a helyzet. A problémák összehasonlítása azonban rávilágít arra, hogy a viszonyítási pont, ahonnan az opciókat (most nem azokra gondolok) megítélhetjük, mindennél fontosabb.
Tehát az alábbi két állítás ugyan a vagyon hasznosságát illetően azonos, megítélésre mégis különbözik:
- A meglévő pénzed mellé kapsz még 1000 dollárt. Majd el kell döntened, hogy 50%-os eséllyel kapsz még 1000 dollárt vagy biztosan 500 dollárt.
- A meglévő pénzed mellé kapsz még 2000 dollárt. Ismét döntened kell, de most arról, hogy 50%-os eséllyel elveszítesz 1000 dollárt, vagy biztosan veszítesz 500 dollárt.
Ha megnézed a kettő ugyanaz, mégis a második esetén a veszteséget látod. Mindkét esetben vagy biztosan több pénzünk lesz 1500 dollárral, vagy elfogadunk egy játékot és egyforma esélyünk lesz az 1000 dolláros és 2000 dolláros nyereségre.
A többség az elsőben biztosra menne, a másodikban kockáztatna, mindössze azért, mert a felütés más volt. A keret, amiben a problémát felvázoltuk más volt, így a döntés is más lett, holott a két eset objektíve ugyanaz. Bernoulli itt tévedett. Nem a hasznosság az elsődleges döntést meghatározó kritérium. Magyarán a nyereségekhez és veszteségekhez való viszonyulásunk nem a vagyon értékeléséből ered.
Nem azért örülsz 500 dollár nyereségnek vagy bosszankodsz 500 dollár veszteség felett, mert ettől több vagy kevesebb lesz a vagyonod, hanem szimplán azért, mert szeretünk nyerni és nem szeretünk veszíteni.
"Bernoulli elmélete szerint elegendő ismernünk a vagyon pillanatnyi állapotát, hogy meghatározhassuk a hasznosságát a kilátáselméletben azonban ismernünk kell a viszonyítási állapotot is."
A közvetlen összehasonlításban a veszteségek nagyobbnak tűnnek, mint a nyereségek. Ennek evolúciós okai vannak. Azok az élőlények, amelyek a kínálkozó alkalmaknál fontosabbnak tartják a fenyegető veszélyeket, nagyobb valószínűséggel maradnak életben és hoznak létre utódokat.
Hogy néz ki ez függvényen?
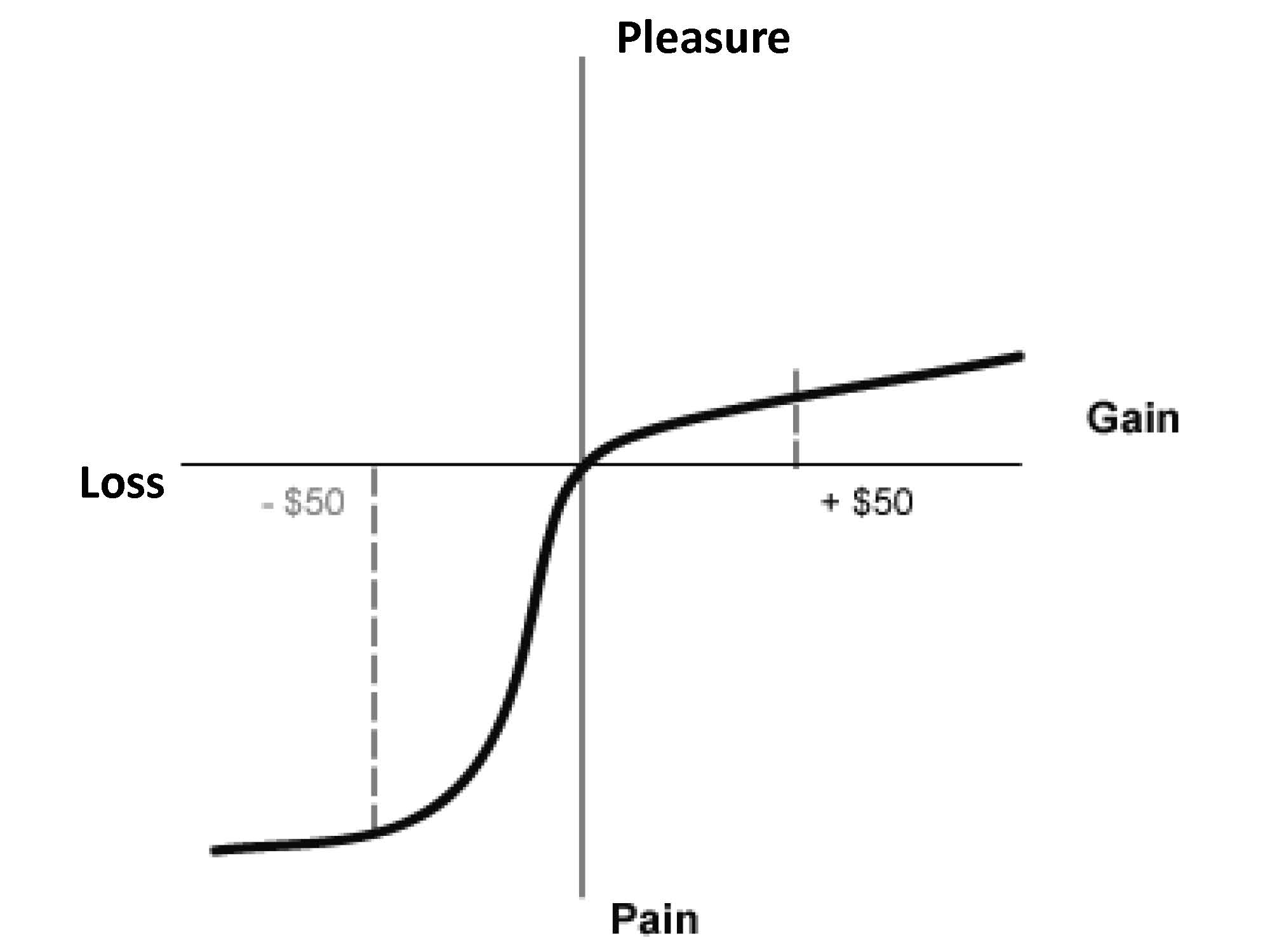
A görbe szembeötlő tulajdonsága, hogy S alakú, azaz a lefutás mind a nyereségekkel, mind a veszteségekkel szembeni csökkenő érzékenységet fejezi ki. A veszteségek erősebb reakciót váltanak ki, mint a hasonló mérvű nyereségek. Ez a jelenség a veszteségkerülés.
Éppen emiatt létezik a volatility skew jelenség, ami nem más, mint az opciók aszimmetrikus árazása. Ez megfigyelhető az SP500 határidős vagy ETF termékben is. A Put oldal sokkal magasabban árazott, mint a call oldal. A 10%-os eséllyel elért strike lefelé sokkal távolabb van mint felfelé. A kezdő azt hiheti, hogy a távolabbi strike magasabb valószínűséget feltételez, de nem. Pont a fenti ábra miatt létezik index szinten volatility skew. Az emberek félnek veszíteni. Sokkal jobban félünk a 10%-os index eséstől, mint amennyire vágyunk a 10%-os index emelkedésre.
Veszteségkerülés
Nézzünk egy egyszerű játékot ismét.
Legyen egy fej vagy írás játék. Ha fej, veszítesz 100 dollárt, ha írás, nyersz 150 dollárt.
Ez esetben a 150 dollár elrakásának pszichológiai előnyét kell szembeállítani a 100 dollár elvesztésének érzelmi költségével. Egyértelműen látható, hogy 50%-os esély mellett (tegyük fel élére nem eshet az érme) a játék várható értéke pozitív, mégis sokan döntenének úgy, hogy nem elég vonzó. Ez a kereskedés során az 1.5 risk reward.
Nagyobb statisztikai mintavétel után kimutatták, hogy az emberek 1:2 körül kezdenek el igazán mérlegelni. Azaz 200 dollár nyerés 100 vesztésével szemben az a szint, ahol elkezd a dolog vonzóvá válni. Ezt hívják veszteségkerülési hányadosnak. Az emberek veszteségkerülők!

Tehát a veszteségkerülést a vagyon hasznosságával magyarázni próbáló érvelés képtelen és kudarcra van ítélve.
Útravaló
- Olvasd el a fenti könyvet, sokat fogsz belőle tanulni a gondolkodásodról. (készülj fel, nehéz)
- Figyelj a túlzott kockázatvállalásra, ha veszteséges helyzetben vagy, mert ez egy lefelé húzó spirál.
- Legyél tudatos a döntéseid során!